高一數學均方差(標準差)公式
標準差(Standard Deviation)，在概率統計中最常使用作為統計分布程度(statistical dispersion)上的測量。標準差定義是總體各單位標志值與其平均數離差平方的算術平均數的平方根。它反映組內個體間的離散程度。測量到分布程度的結果，原則上具有兩種性質：
為非負數值， 與測量資料具有相同單位。一個總量的標準差或一個隨機變量的標準差，及一個子集合樣品數的標準差之間，有所差別。
標準計算公式
假設有一組數值X1,X2,X3,......XN(皆為實數)，其平均值為μ，公式如圖1.
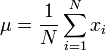
圖1
標準差也被稱為標準偏差，或者實驗標準差，公式如圖2。
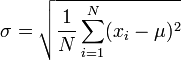
圖2
簡單來說，標準差是一組數據平均值分散程度的一種度量。一個較大的標準差，代表大部分數值和其平均值之間差異較大;一個較小的標準差，代表這些數值較接近平均值。
例如，兩組數的集合 {0,5,9,14} 和 {5,6,8,9} 其平均值都是 7 ，但第二個集合具有較小的標準差。
標準差可以當作不確定性的一種測量。例如在物理科學中，做重復性測量時，測量數值集合的標準差代表這些測量的精確度。當要決定測量值是否符合預測值，測量值的標準差占有決定性重要角色：如果測量平均值與預測值相差太遠(同時與標準差數值做比較)，則認為測量值與預測值互相矛盾。這很容易理解，因為如果測量值都落在一定數值范圍之外，可以合理推論預測值是否正確。
標準差應用于投資上，可作為量度回報穩定性的指標。標準差數值越大，代表回報遠離過去平均數值，回報較不穩定故風險越高。相反，標準差數值越小，代表回報較為穩定，風險亦較小。
例如，A、B兩組各有6位學生參加同一次語文測驗，A組的分數為95、85、75、65、55、45，B組的分數為73、72、71、69、68、67。這兩組的平均數都是70，但A組的標準差為17.078分，B組的標準差為2.16分(此數據是在R統計軟件中運行獲得)，說明A組學生之間的差距要比B組學生之間的差距大得多。
如是總體，標準差公式根號內除以n
如是樣本，標準差公式根號內除以(n-1)
因為我們大量接觸的是樣本，所以普遍使用根號內除以(n-1)
公式意義
所有數減去其平均值的平方和，所得結果除以該組數之個數(或個數減一，即變異數)，再把所得值開根號，所得之數就是這組數據的標準差。
深藍區域是距平均值小于一個標準差之內的數值范圍。在正態分布中，此范圍所占比率為全部數值之 68%。根據正態分布，兩個標準差之內(深藍，藍)的比率合起來為 95%。根據正態分布，三個標準差之內(深藍，藍，淺藍)的比率合起來為 99%。
(責任編輯：張新革)
分享“高一數學均方差(標準差)公式”到：
