2011同等學力申碩考前30練：計算機綜合數學

    一、形式化下列語句

    1. 有的實數不是有理數，但所有的有理數都是實數。

    2. 對于任意實數都存在比它大的實數 .

    3. 若那套房子有三室一廳，并且居住面積在90平米以上，老王就要那套房子。

    4. 每位父親都喜歡自己的孩子。

    二、填空

    1. 設p：1＋1＝5，q：明天是陰天，則命題"只要1＋1＝5，那么明天是陰天"可符號化為_____________，其真值是________.

    2. 在公式（  z）（P（z）→Q（x，z））∧（  z）R（x，z）中，  z的轄域是___________________， z的轄域是__________________.

    3. 設R為非空集合A上的二元關系，如果R具有自反性。___________.__________則稱R為A上的一個偏序關系。

    4. 設x＝{1，3，5，9，15，45}，R是x上的整除關系，則R是x上的偏序，其最大元是___________，極小元是_________.

    5. 給定命題公式（P∨Q）→R，該公式在聯接詞集合{  ，→}中的形式為__________，在聯接詞集合{  ，∧}中的形式為__________ .

     6. 設 ， 中可定義_______個函數，其中有_________個滿射函數；

     可定義_______個函數，其中有_________個單射函數。

    7. 設x＝{1，3，5，9，15，45}，R是x上的整除關系，則R是x上的偏序，其最大元是_________，極小元是______.

    8. 6名志愿者分配到5個西部學校支教，每個學校至少1人，共有_____種不同的分配方式。

    三、判斷下列推理式及集合。關系運算的正確性

   1. （P→Q） （P→R）   P →（Q  R） （   ）

    2. （P Q）→R  （P→R）  （Q→R） （   ）

    3. 一個關系可以：既不滿足自反性，也不滿足非自反性。（   ）

    4. 一個關系可以：既不滿足對稱性，也不滿足反對稱性。（   ）

    5. 一個關系可以：既滿足對稱性，同時也滿足反對稱性。（   ）

    四、計算和證明

    1. 設個體域D＝{2，3，6}，F（x）：x≤3，G（x）：x>5，消去公式 x（F（x）∧ yG（y））中的量詞，并討論其真值。

    2. 用等值演算法求公式 （p→q）→（p→q）的主合取范式。

    3. 設A=  ，（1）求P（A）；（2）寫出P（A）上的包含關系 .

    4. 設  ，從A到B不同的二元關系有多少個？ 又有多少種不同的函數？

    5. 設 ，在A×A上定義關系R：如果a+d=b+c， 則<a， b>R<c， d>.（1）證明R是等價關系。（2）求[<3，6>]R .

    6. 設 ，R是集合A上的整除關系： R＝{<x，y>| x整除y }.（1）證明R是偏序關系； （2）畫出相應的哈斯圖。

    7. 設A＝{a，b，c}，求A上所有等價關系。

    8. 所有的主持人都很有風度。李明是個學生并且是個節目主持人。因此有些學生很有風度。請用謂詞邏輯中的推理理論證明上述推理。（個體域是人）

    9. 求  的主析取范式。

    10. 有向圖D=<V，E>如圖所示

    1）D中有多少條不同的初級回路；

    2）求v1到v4的短程線與距離；

    3）判斷D是哪一類連通圖。

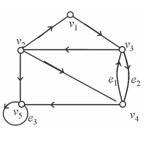
    11. 求由2個0.3個2和3個5構成的八位數共有多少個？

    12. 一棵無向樹T中有ni個頂點的度數為i， i=1，2，3，…，k，其余頂點都是葉子，試計算T中的葉子數。

    13. 證明題構造下面推理的證明：

    前提： 

    .結論：  

    下載原題： 

  2011年同等學力計算機綜合數學.doc

8c89225f85d7bf66aa495cad89402cdc.doc (63.50 KB)