2017考研數(shù)學(xué)基礎(chǔ):逆序數(shù)和行列式的定義分析

 2017考研數(shù)學(xué)基礎(chǔ):逆序數(shù)和行列式的定義分析

    行列式是線性代數(shù)的基本概念和工具，它在矩陣可逆性的判斷、線性方程組的求解、特征值的計(jì)算以及二次型是否正定的判斷等方面都有重要作用。行列式的計(jì)算是基于行列式的一些性質(zhì)，而性質(zhì)又是根據(jù)行列式的定義推導(dǎo)出來(lái)的，因此，為了使大家更好地理解行列式的性質(zhì)和計(jì)算方法，文都考研老師對(duì)行列式的定義及其相關(guān)的逆序數(shù)概念和性質(zhì)做些分析，供同學(xué)們學(xué)習(xí)參考。

　　一、逆序數(shù)

　　定義：在n個(gè)元素的一個(gè)排列中，當(dāng)某兩個(gè)元素的次序與標(biāo)準(zhǔn)次序(對(duì)整數(shù)的排列一般以從小到大的次序作為標(biāo)準(zhǔn)次序)不同時(shí)，就稱(chēng)為1個(gè)逆序，逆序的總數(shù)稱(chēng)為該排列的逆序數(shù)。

　　例如：排列312的逆序有31，32，其逆序數(shù)為2;排列2413的逆序有21，41，43，其逆序數(shù)為3.

　　當(dāng)逆序數(shù)為奇數(shù)時(shí)，稱(chēng)為奇排列，當(dāng)逆序數(shù)為偶數(shù)時(shí)，稱(chēng)為偶排列。

　　如果對(duì)排列的次序作改變，則排列的奇偶性有如下性質(zhì)：

　　定理：對(duì)換排列中的兩個(gè)元素，排列的奇偶性改變。

    在上面n階行列式的定義中，用到了排列的逆序數(shù)這個(gè)概念，關(guān)于逆序數(shù)的定理及其推論，在以后分析證明行列式的性質(zhì)中會(huì)用到。對(duì)于任意一個(gè)n階行列式，雖然從理論上按照定義可以計(jì)算出其值，但當(dāng)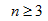時(shí)，其計(jì)算量比較大，并且也容易出錯(cuò)，因此一般不用定義計(jì)算，而是運(yùn)用行列式的有關(guān)性質(zhì)計(jì)算，這些性質(zhì)文都考研蔡老師后續(xù)會(huì)進(jìn)行分析總結(jié)，請(qǐng)大家進(jìn)一步關(guān)注。