公務員考試培訓網

    30÷（4-1）=10（米），

    長的電線長

    10+30=40（米）或10×4=40（米）。

    答：短的電線長10米，長的電線長40米。

    解差倍應用題的關鍵是確定“1倍”數是誰，“差”是什么。上兩例中，“1倍”數及“差”都極明顯地直接給出。下面講兩個稍有變化，不直接給出“差”和“1倍”數的例子。

    例3 甲、乙二工程隊，甲隊有56人，乙隊有34人。兩隊調走同樣多人后，甲隊人數是乙隊人數的3倍。問：調動后兩隊各還有多少人？

    分析：畫線段圖如下：

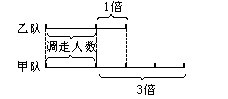
    由上圖可知，“1倍”數是乙隊調動后剩下的人數。因甲、乙隊調走的人數相同（不影響他們二隊人數之差），所以，甲、乙兩隊人數之差仍是56-34=22（人）。

    解：由差倍公式得調動后乙隊有

    （56-34）÷（3-1）=11（人）。

    調動后甲隊有

    11×3=33（人）或11+（56-34）=33（人）。

    答：調動后甲隊有33人，乙隊有11人。

    例4 甲、乙兩桶油重量相等。甲桶取走26千克油，乙桶加入14千克油，這時，乙桶油的重量是甲桶油的重量的3倍。兩桶油原來各有多少千克？

    分析與解：畫線段圖如下：

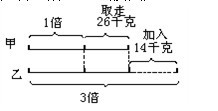
    從上圖知，當甲桶取走26千克、乙桶加入14千克后，乙桶里的油就是甲桶里的油的3倍，所以，“1倍”數是甲桶里剩下的油。“差”是什么呢？從圖中可知，“1倍”與“3倍”之間的差26+14=40（千克）就是我們要找的“差”。所以，由差倍公式知，

    “1倍”數=（26+14）÷（3-1）=20（千克）。

    故甲、乙桶原來各有油

    20+26=46（千克），

    或 20×3-14=46（千克）。

    答：原來各有46千克。

    例5 小云比小雨少20本書，后來小云丟了5本書，小雨新買了11本書，這時小雨的書比小云的書多2倍。問：原來兩人各有多少本書？

    分析與解：“小雨的書比小云的書多2倍”，即小雨的書是小云的書的3倍。這個“倍數”是變化后的，所以“1倍”數應是小云變化后的書（見下圖）。“差”是

    20+5+11=36（本）。

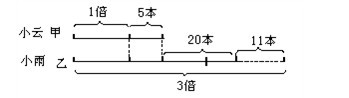
    根據和差公式得：

    小云現有書

    （20+5+11）÷（3-1）=18（本）。

    小云原來有書18+5=23（本），

    小雨原來有書23+20=43（本）。

    答：原來小云有23本書，小雨有43本書。